Using Stan to analyse global UFO sighting reports

UFO sighting data
A recent #TidyTuesday data set piqued my interest. It’s a rather large collection of worldwide reportings of UFO sightings.
Interesting.
You can download the data yourself and load it into R:
library("readr")
ufo_sightings = read_csv("ufo_sightings.csv")
ufo_sightings contains information about thousands of UFO sightings. Each sighting contains information such as the date and time (reported_date_time, day_part) of the sighting, the location (city, state, country) of the sighting, and other information such as a freetext summary. The summary column is by far the most interesting …
library("dplyr")
ufo_sightings %>%
select(city, day_part, summary) %>%
head()
# A tibble: 6 × 3
city day_part summary
<chr> <chr> <chr>
1 Pinehurst night Saw multi color object above horizon.
2 Rapid City nautical dusk An object in the shape of a straight line about an …
3 Cleveland night Tone in the air.
4 Bloomington afternoon Black tic-tac shaped ufo. Moved with insane speed
5 Irvine night Two alien were scanning me
6 Moore morning Long cigar solid shaped craft with light beam
What do we want to achieve?
The goal here is to fit a simple Bayesian model which will allow us to understand the historical counts of reported UFO sightings. The Bayesian approach to modelling is a probabilistic approach to modelling that has some advantages:
- we are able to incorporate meaningful prior information about model parameters
- including uncertainty in our predictions is natural and automatic.
A common drawback of Bayesian methods is the lack of fast and simple-to-use software to fit such models. With modern tools such as Stan, fitting Bayesian models is less of a headache!
We’re going to use Stan to fit our model, but I’ll be sparing you the details of the program, as well as many other details — we’ve linked to a Github repo at the end of this post with full analysis scripts. The purpose of this post is to give a high level overview of how we can fit flexible regression models for count data using Stan. We also touch upon how to work with Markov chain Monte Carlo (MCMC) output within a {tidyverse} framework towards the end of this post.
What is Stan?
Stan is a free, open source, C++ program used for specifying and fitting Bayesian models. Stan uses state of the art MCMC algorithms to fit your Bayesian models, thus is efficient and numerically stable. We don’t really have the time to delve too much into the reasons for using Stan today, but this previous post goes into considerable detail! If you’ve used JAGS or PyMC3 before, the concept behind Stan is similar; you specify your Bayesian model in the Stan language, and Stan takes care of the MCMC algorithm for you. Installing Stan is simple in R; calling
install.packages("rstan", dependencies = TRUE)
will install Stan for you (as well as the {rstan} package).
A note on how to interpret the analysis
It’s definitely worth stating up front that the purpose of this post is to have a little play with Stan and a fun data set. This data set contains reported UFO sightings, they’re not confirmed UFO sightings. Therefore, we can only make statements about reports and not the numbers of UFOs.
Let’s take a peek at the data
Prior to modelling the yearly counts, we should have a little look at the data. This can help us make informed modelling choices later down the line.
The number of sightings per year isn’t directly recorded in this data, but we can wrangle this out of the raw data with a few {dplyr} commands. We also only look at the GB data.
library("tibble")
library("lubridate")
library("dplyr")
sights_per_year = ufo_sightings %>%
filter(country_code == "GB") %>%
mutate(year_of_sighting = year(reported_date_time)) %>%
summarise(
sightings_per_year = length(year_of_sighting),
.by = "year_of_sighting"
) %>%
complete(
year_of_sighting = full_seq(year_of_sighting, 1),
fill = list(sightings_per_year = 0)
)
We’ve now got annual counts of the number of global sightings. The first date in the data set is 1938, so the counts start from then.
Okay, let’s plot the data:
library("ggplot2")
sights_per_year %>%
ggplot() +
geom_point(aes(x = year_of_sighting,
y = sightings_per_year)) +
xlab("Year of reported sighting") +
ylab("Number of recorded sightings per year") +
ggtitle("Yearly UFO sighting reports for Great Britain") +
theme_minimal()
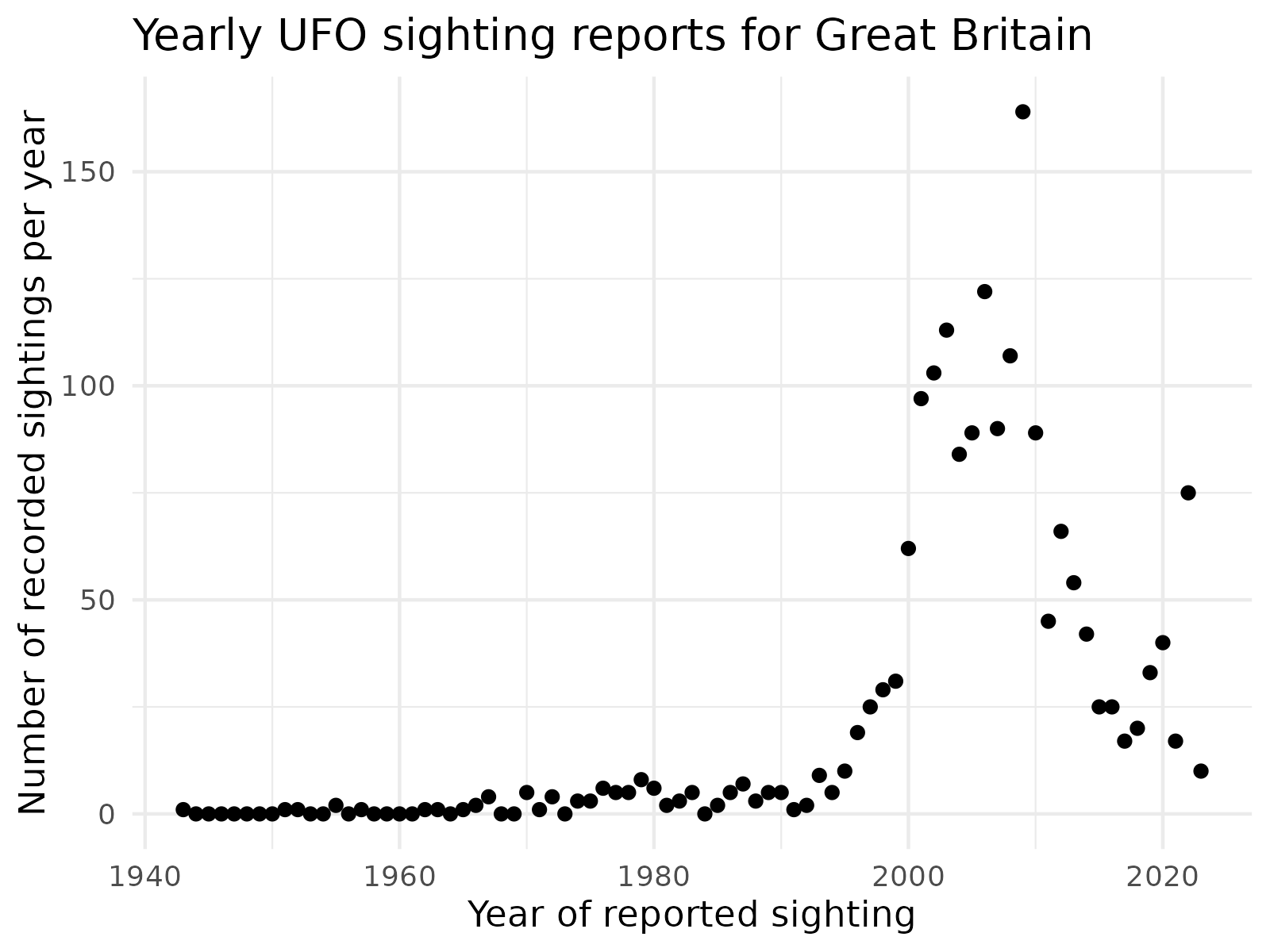
There are a few interesting features of the data set:
- The data produces a complex pattern; this might be tricky to model!
- The number of reports pre 2000 was generally small.
- The number of reports increases from roughly the year 1995 until the late 2000s.
- From 2010 onward, the number of reports is in rapid decline.
To be honest, I’m not really sure why we see a rapid increase of sightings from the mid 90s onwards. There are a few potential reasons for this:
- There was an increase in UFO traffic over Earth from the mid 1990s to 2010 (maybe 👽)
- The emergence of the internet brought like-minded people together, improving the ease of reporting (plausible)
- The 1996 blockbuster Independence Day had some kind of effect on people (plausible)
The statistical approach
Our approach here will be to model the number of UFO sighting reports over time with a Negative Binomial regression model, using spline terms to flexibly model the non-linear trend. This wasn’t the first idea I had, but after a little bit of frustration, contemplation and iteration, this gave a reasonably good fit to the data.
Some previous approaches (we won’t delve into the details) involved simpler Poisson models.
The statistical model is as follows:
\( y\mid \lambda(X) \sim \text{NegBin} (\lambda(X), \phi) \)
\( \log \lambda(X) = \alpha + X\beta \)
Where \(y\) is the number of sightings, \(X\) is a matrix of spline terms (derived from the times at which sightings were observed), \(\lambda(X)\) is the expected number of sightings and \(\phi \) is a dispersion parameter. A model block in Stan for this statistical model might look a bit like this:
// Stan model block
model {
// likelihood
y ~ neg_binomial_2_log(alpha + X * beta, exp(log_phi));
// prior
alpha ~ normal(m_alpha, s_alpha); // intercept
beta ~ normal(m_beta, s_beta); // spline coefficients
log_phi ~ normal(m_phi, s_phi); // log dispersion term
}
There’s quite a bit going on here. Let’s break the model down a little:
- The
neg_binomial_2_logdistribution is used to specify the likelihood. This is an alternative parameterisation of the Negative Binomial distribution; the first parameter ofneg_binomial_2_logis \( \log {E (y \mid X, \alpha, \beta, \phi)} \), the second parameter is simplyphi. - The
2inneg_binomial_2_logtells us that this distribution is parameterised by the mean and dispersion (rather than by the shape and scale parameters). - The
logtells us that we’re actually parameterising by the log mean, rather than raw mean. alphais an intercept term (for a linear predictor);betais a vector of regression coefficients.
In our approach, we’re going to use R to generate spline terms for us, then pass these spline terms to Stan (and thus populate X). If you’re unfamilliar with splines, they’re clever devices which allow us to model non-linear behaviour. This crs vignette provides an introduction. Another approach would be to write a Stan function to construct the splines, as in this Stan case study. The advantage of the approach we’ve taken is that splines are not a hard coded feature of the model, so we could use this Stan program for a more general Negative Binomial regression. The downside is, if someone used this Stan model as part of a workflow not performed with R, we would have to carefully verify that splines have been constructed in the same way as the R implementation.
Constructing the Splines
From a data preparation perspective, the trickiest thing is probably constructing the B spline basis functions (the other parts of our Stan program can simply be specified). However, the bs() function from the {splines} package takes the hard work out of this. The following function call constructs our splines for us; we’ve specified that we want to use 10 ‘knots’ which are a part of the specification of our spline terms. We could try many numbers of knots and use model selection methods to pick the best number (or even model averaging methods), but we later see that 10 knots provides a reasonable fit of the data.
library("splines")
year_range = range(sights_per_year$year_of_sighting)
B = bs(sights_per_year$year_of_sighting,
knots = seq(from = year_range[1],
to = year_range[2],
length = 10),
degree = 3,
intercept = TRUE)
Once we’ve done this, we’re basically ready to run our Stan program. All we need to do is collect all of our data together in a list, we’ve called this stan_data.
Performing the inferences
To perform our inferences, we’re going to use Stan with help from {rstan}. {rstan} provides an interface to Stan from R, as well as some other handy features like plotting functions. A bit of trial and error led me to use a thinning factor of 10 in the MCMC scheme, and a warmup period of 1000 proved to be adequate, so we’ll use these numbers again, and aim to have 4 (approximately) unautocorrelated chains of length 5000. If you’ve never used MCMC methods before, we typically specify a warmup (or “burn in”) period to account for the fact that an MCMC chain must “converge” to the region of high posterior density, from the chains starting point. The thinning factor is used to account for the fact the Markov chains exhibit a dependence structure (like a time series might), if we keep only every thin-th iteration, we can reduce, or even eliminate, the autocorrelation in the chain. These steps allow us to better assess the quality of the MCMC scheme and also reduce computational overheads. If we didn’t thin, and kept the warmup period, we can end up with a very memory-intensive MCMC chain.
This is achieved with the following code. Our Stan program is in the file stan/nbin_reg.stan.
library("rstan")
options(mc.cores = 4) ## run chains in parallel (using 4 cores)
target_iter = 5000
warmup = 1000
thin = 10
total_iter = warmup + thin * target_iter
K = ncol(B)
stan_data = list(
N = nrow(sights_per_year),
K = K,
y = sights_per_year$sightings_per_year,
X = B,
# priors
m_alpha = 0,
s_alpha = 1,
m_beta = rep(0, K),
s_beta = rep(1, K),
m_phi = 0,
s_phi = 1
)
fit = stan(
"stan/nbin_reg.stan",
data = stan_data,
chains = 4,
iter = total_iter,
warmup = warmup,
thin = thin
)
Making the Stan output a bit more usable
The object fit is a stanfit object (an S4 class). These can be a bit awkward to work with, but {tidyverse} fans will find the {tidybayes} package offers a natural approach to working with MCMC output. Suppose our Stan program performs sample prediction at the years at which we observed the data via the following genreated quantities block. The _rng suffix on the neg_binomial_2_log_rng tell us we are performing random sampling from the neg_binomial_2_log distribution.
generated quantities {
int y_pred[N];
y_pred = neg_binomial_2_log_rng(log_lambda, exp(log_phi));
}
We might want to plot the summaries of the distribution of y_pred over time (or e.g. posterior quantiles as a function of time). In it’s raw format, wrangling this data from fit is a bit clunky. However, the tidybayes::spread_draws() function makes this simple! The only unusual thing to remember is that, if y_pred is a vector or array (in Stan), then we need to append [condition] to the column name (in R) to preserve the fact that a y_pred is many draws of an array of dimension N.
## [condition] tells tidybayes to group by index of y_pred
tidy_fit = fit %>%
spread_draws(y_pred[condition])
head(tidy_fit)
# A tibble: 6 × 5
# Groups: condition [1]
condition y_pred .chain .iteration .draw
<int> <dbl> <int> <int> <int>
1 1 0 1 1 1
2 1 0 1 2 2
3 1 0 1 3 3
4 1 3 1 4 4
5 1 0 1 5 5
6 1 2 1 6 6
We see here that, although we only have one “statistical” variable (y_pred), we have quite a few pieces of metadata. Firstly, we have condition - this is the element of y_pred that we have repeated samples from. .chain refers to the MCMC chain, .iteration is the draw within that chain, and .draw is essentially a unique id for each row of tidy_fit. The y_pred column is the randomly drawn value of y_pred at the chain-iteration combination.
The nice thing here is that because our Stan output is a tibble, we can use all of our favourite {tidyverse} tools to summarise the Stan output.
For example, to see which years had the largest posterior mean number of sightings, we can use the following snippet:
tidy_fit %>%
reframe(mean = mean(y_pred),
year = year_of_sighting) %>%
distinct() %>%
arrange(-mean) %>%
head(5)
# A tibble: 5 × 3
condition mean year
<int> <dbl> <dbl>
1 45 119. 2006
2 44 118. 2005
3 46 114. 2007
4 43 109. 2004
5 47 103. 2008
From this, we can see that the UFO haydays were the mid 2000s. Of course, plotting the data and predictions will give us a more complete picture. Similar logic would allow us to determine which spline terms were the most important; grabbing the \( \beta\) terms (coefficients of spline terms), and ordering by \( | E(\beta \mid \mathcal{D}) | \) is one approach to determining which spline terms are most important:
fit %>%
spread_draws(beta[condition]) %>%
summarise(mean_beta = mean(beta)) %>%
arrange(-abs(mean_beta)) %>%
head(3)
# A tibble: 3 × 2
condition mean_beta
<int> <dbl>
1 10 4.11
2 3 -2.21
3 5 -2.04
We see here that the 10th spline term is the most imporant, followed by the 3rd and 5th. Because MCMC algorithms are stochastic, your results might be slightly different to mine, but the main messages should be very similar.
Again, those familiar with {tidyverse} packages will find that {tidybayes} makes plotting posterior summaries of the data relatively straight forward
tidy_fit %>%
ggplot(aes(x = year_of_sighting, y = sightings_per_year)) +
stat_lineribbon(aes(y = y_pred), .width = c(.97, .89, .73, .5), colour = "grey10") +
scale_fill_brewer() +
geom_point(aes(x = year_of_sighting, y = sightings_per_year), data = sights_per_year) +
xlab("Year of reported sighting") +
ylab("Number of recorded sightings per year") +
ggtitle("UFO sighting reports for Great Britain,\nwith posterior summaries superimposed") +
guides(fill = guide_legend(title = "Posterior\ncoverage")) +
theme_minimal()
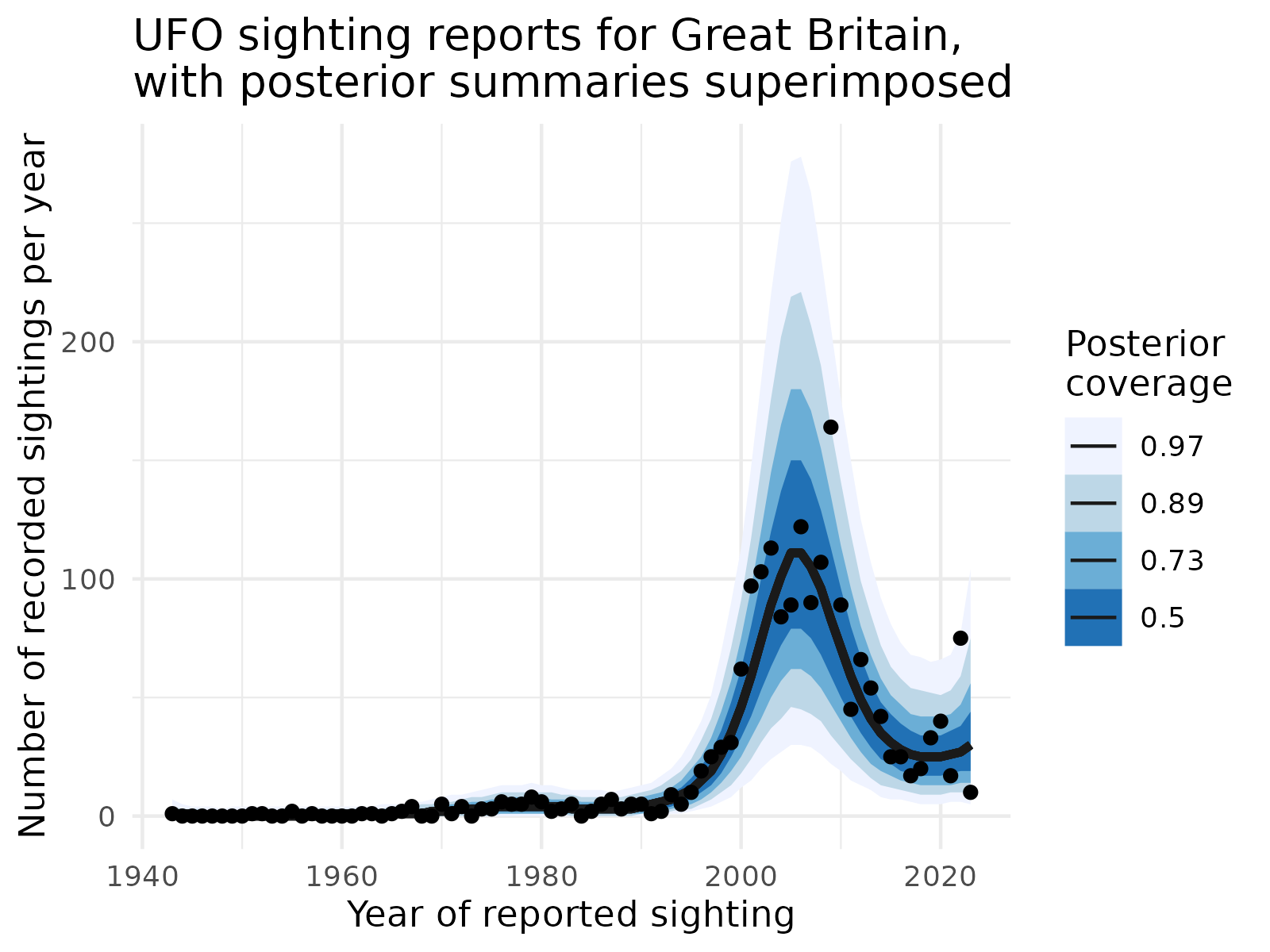
From our plot, we see that indeed, the mid 2000s were the peak for UFO sightings, and the model has captured this quite well. Uncertainty quantification is also good; we see that only a small number of points lie outside the 89% and 97% predictive bands. The median line (50%) follows the trend of the data closely and is also fairly smooth!
Summary
We’ve had a whirlwind tour of fitting flexible models for count data in Stan, and how to process the output using R and {tidybayes} to communicate our findings. UFO sightings certainly boomed during the 2000s, but in recent years, the skies appear to be a somewhat empty. We only performed the analysis for the GB subset of the data. What would be interesting (but would take a while!) would be to construct a joint model for UFO sightings across all countries. We could then, for example, cluster the posterior distributions for curves to identify similar trends. This could allow us to investigate the Independence Day effect; if the effect is real, we would expect to see similar patterns in countries where Independence Day was popular. Of course, the same effect could be explained by other hypotheses!
We didn’t show you all the code to run the Stan model, you can find a complete R script and Stan file to perform the analysis in our blogs repo. As mentioned, the MCMC algorithm is stochastic, so there may be small discrepancies between your results and mine.
If you think Stan is awesome and want to learn more, then why not consider attending one of our Rstan or PyStan courses? Our courses are a great hands-on and interactive way of getting up-and-running and fitting models with Stan!

